【强化学习】强化学习，第4部分：基于MDP的最优策略搜索 |

语言 Chinese, Simplified

SEO Title

Reinforcement Learning, Part 4: Optimal Policy Search with MDP

最优策略搜索：代理如何选择最佳路径

现在我们了解了MDP，我们可以将其视为代理工作的环境。为了随着时间的推移获得最大的回报，该代理需要找到一个最优策略。也就是说，它必须确定在每个州采取的最佳行动。

⏩ 最优策略：在每个州采取最佳行动，随着时间的推移获得最大回报

为了帮助我们的代理做到这一点，我们需要两件事：

一种确定MDP中状态值的方法。
在特定状态下采取的行动的估计值。

1.贝尔曼最优性方程

贝尔曼最优方程为我们提供了估计每个状态最优值的方法，记为V*（s）。它通过计算一个州可以产生的预期奖励来估计该州的价值。

这是贝尔曼最优方程（状态值函数）：

在哪儿：

P（s，a，s'）是代理选择动作a时从状态s到状态s'的转换概率。
R（s，a，s’）是当代理选择动作a时，从状态s到状态s’的即时奖励。
𝛾 是折扣率。折扣奖励以递归方式编写。

你可能想知道如何将我上一篇文章中介绍的折扣奖励转换为递归符号。也许下面的计算过程会给你一个提示。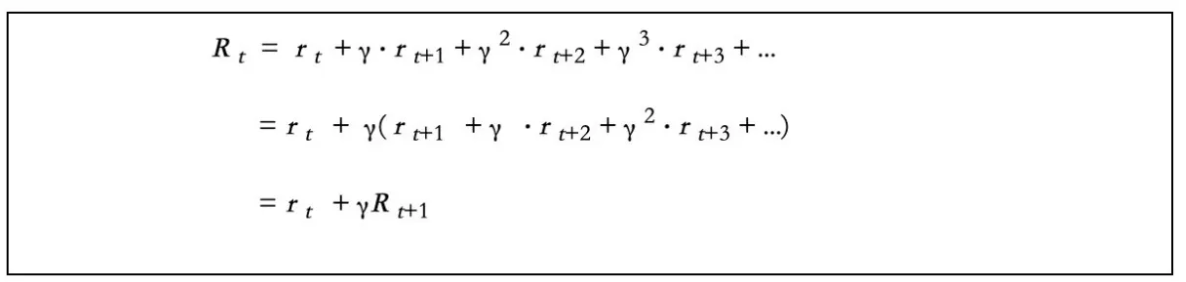

在实践中，您可以首先将所有状态值估计值初始化为零。然后，您使用上述公式计算的结果迭代地更新它们。这将证明是趋同的。

2.Q值迭代算法

仅凭最优状态值并不能告诉代理在每个状态下采取什么行动。幸运的是，受上述最优状态值概念的启发，Bellman为我们提供了一个类似的公式来估计状态-动作对的值，称为Q-value。

⏩ Q值：在状态s采取的行动a的估计值；记为Q*（s，a）

根据Q值得分，Q值明确地“告诉”代理人在每个状态下应该选择哪个动作。

以下是如何计算Q值：

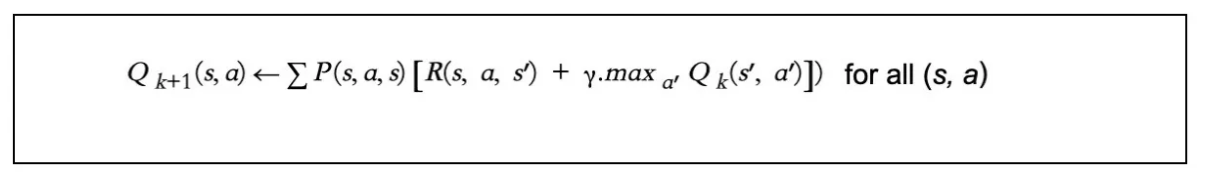
在哪儿：

P（s，a，s'）是代理选择动作a时从状态s到状态s'的转换概率。
R（s，a，s’）是当代理选择动作a时，从状态s到状态s’的即时奖励。
𝛾 是折扣率。折扣奖励以递归方式编写。
max a'Qk（s'，a'）是状态s下最佳动作a'的值

注意：此函数假设代理在当前状态下选择操作后，其行为最佳。

与Bellman Optimality EquaEquation练习一样，您将首先将所有Q值估计值初始化为零。然后，使用此公式计算的结果迭代更新它们。

最优策略搜索的MDP实现

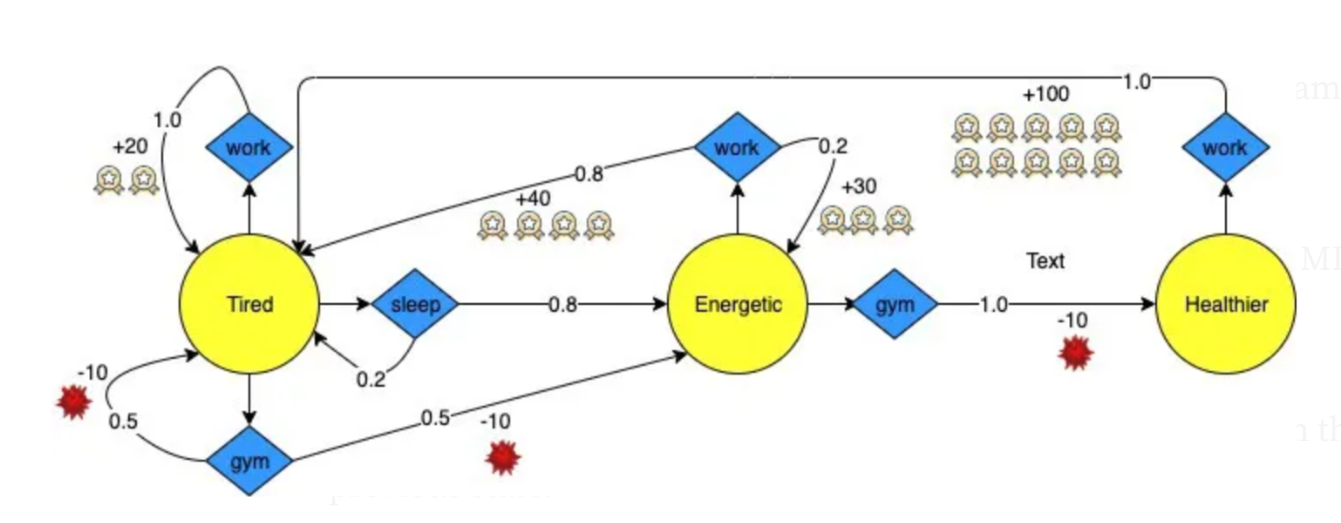
现在，让我们将所学付诸实践！我们将使用上图中朋友Adam的MDP来运行最优策略搜索。

首先，我们输入5元组（S，A，P，R，𝛾) 在我们的演示中创建MDP环境。

我们用nan来表示我们无法从前一个状态到达的状态。
变体动作是A。形状为（s，A）的动作空间是一个二维数组。
P表示从状态s到状态s'的转换概率，选择动作a。它的形状应该是（s，a，s'），一个三维数组。
R代表从状态s转换到s'后，由于动作a而获得的即时奖励。它的形状应该是（s，a，s'），一个三维数组。

import numpy as npnan = np.nanactions = [[0, 1, 2], [0, 2], [0]]P = np.array([[[1.0, 0.0, 0.0], [0.2, 0.8, 0.0], [0.5, 0.5, 0.0]],[[0.8, 0.2, 0.0], [nan, nan, nan], [0.0, 0.0, 1.0]],[[1.0, 0.0, 0.0], [nan, nan, nan], [nan, nan, nan]],])R = np.array([[[20., 0.0, 0.0], [0.0, 0.0, 0.0], [-10., -10., 0.0]],[[40., 30., 0.0], [nan, nan, nan], [0.0, 0.0, -10.]],[[70., 0.0, 0.0], [nan, nan, nan], [nan, nan, nan]],])

现在我们有了MDP环境！

让我们使用Q值迭代算法来获得Q*（s，a），其中包含状态s下动作a的得分。

我们使用-inf来表示我们不能在状态s中采取的操作。
用零初始化Q*（s，a）。
对于每次迭代，将Q值公式应用于从状态s到状态s'的每次转换，采取行动a，并用新结果更新Q*（s，a）。

Q = np.full((3, 3), -np.inf)
for s, a in enumerate(actions):
   Q[s, a] = 0.0

discount_factor = 0.99
iterations = 10
for i in range(iterations):
   Q_previous = Q.copy()
   for s in range(len(P)):
       for a in actions[s]:
           sum_v = 0
           for s_next in range(len(P)):
               sum_v += P[s, a, s_next] * (R[s, a, s_next] +
                         discount_factor * np.max(Q_previous[s_next]))
           Q[s, a] = sum_v
print(Q)

以下是我们得到的Q：