【强化学习】强化学习，第5部分：蒙特卡洛和时间差异学习

我强化学习系列的前几篇文章：

• RL简介
• 介绍马尔可夫过程
• 马尔可夫决策过程
• 基于MDP的最优策略搜索

现在我们已经介绍了MDP，是时候讨论Q学习了。为了发展我们对这一主题的了解，我们需要逐步了解：

• 动态规划（DP）：在我们对MDP的讨论中引入
• 蒙特卡罗（MC）学习：在信息缺乏时进行适应
• 最简单的时间差学习，TD（0）：DP和MC的组合

一旦我们介绍了蒙特卡洛和时间差分学习，我们将到达更著名的Q学习。

让我们开始吧！

MDP与动态规划

在我的系列文章的最后几部分，我们一直在学习如何用马尔可夫决策过程（MDP）解决问题。为此，我们使用动态规划（DP）评估给定的策略，并通过连续迭代得出最优值函数。

让我们列出并回顾一些关键术语，以帮助我们继续进行：

• 动态规划：将一个大问题分解为增量步骤，以便在任何给定阶段都能找到子问题的最优解
• 模型：现实世界过程的数学表示（见第3部分中的“与亚当一起学习”）
• 贝尔曼最优方程：为我们提供了估计每个状态最优值的方法（见第4部分）
  现在需要注意的是，MDP只适用于已知的模型，其中所有五个元组（如下所示）都是显而易见的。

从本文开始，我们将着手解决当模型的一部分未知时的MDP问题。

在这种情况下，我们的代理必须通过与环境交互并收集经验或样本来从环境中学习。在此过程中，代理进行策略评估和迭代，可以获得最优策略。

由于支持这种方法的理论来自蒙特卡洛方法，让我们从讨论蒙特卡洛学习开始。

蒙特卡洛学习

我们已经了解到，整个问题可以转化为马尔可夫决策过程（MDP），该过程使用上述五个元组<s，P，a，R，γ>做出决策。

当我们知道这五个因素时，就很容易计算出获得最大回报的最佳策略。然而，在现实世界中，我们几乎从来没有同时拥有所有这些信息。

例如，状态转移概率（P）很难知道，没有它，我们就无法使用下面的贝尔曼方程来求解V和Q值。

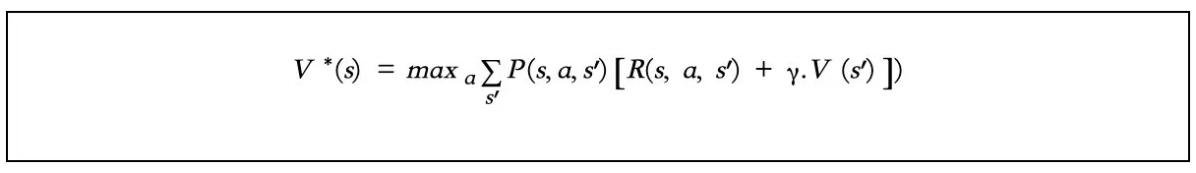
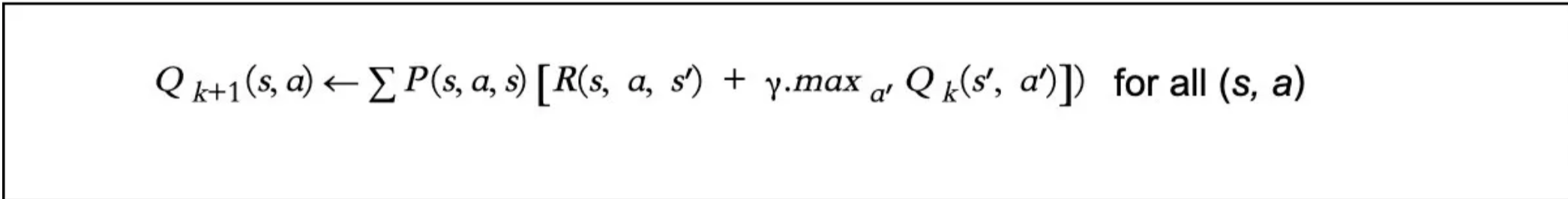
但是，如果我们必须在不知道P的情况下解决一个问题呢？我们如何将其转化为马尔可夫决策过程？

首先，考虑到虽然我们不知道状态转移概率P是什么，但我们客观地知道它的存在。因此，我们只需要找到它。

为此，我们可以让我们的代理运行试验，不断收集样本，获得奖励，从而评估价值函数。这正是蒙特卡洛方法的工作原理：尝试多次，最终估计的V值将非常接近真实的V值。

蒙特卡洛评估

如前所述，蒙特卡洛方法涉及让代理通过与环境交互和收集样本来从环境中学习。这相当于从概率分布P（s，a，s'）和R（s，α）中采样。

然而，蒙特卡罗（MC）估计仅适用于基于试验的学习。换句话说，一个没有P元组的MDP可以通过反复试验来学习。

在这个学习过程中，每一次“尝试”都被称为一集，所有集都必须终止。也就是说，应该达到MDP的最终状态。每个状态的值仅基于最终奖励Gt进行更新，而不是基于邻居状态的估计，如贝尔曼最优方程中所示。

MC从完整的剧集中学习，因此只适用于我们所说的剧集MDP。

以下是我们更新的状态值公式：

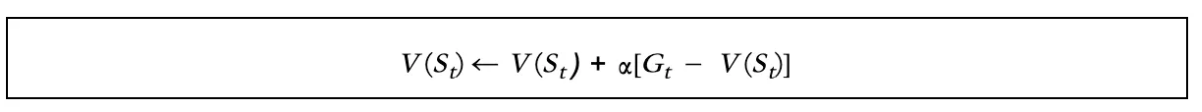
在哪儿：

• V（St）是我们要估计的状态值，可以随机初始化或使用特定策略初始化。

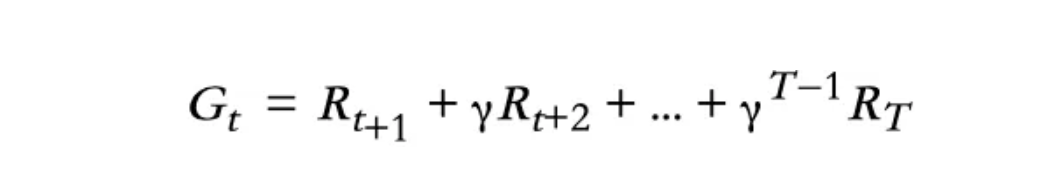
• Gt如上计算，T是终止时间。
• 是一个类似于学习率的参数。它可以影响收敛。
   

获得V（St）的各种方法

考虑一下：如果状态s在事件中分别在时间t+1和时间t+2出现两次，我们在计算状态s的值时是使用一个还是两个？我们多久更新一次V（St）？我们对这些问题的回答将引导我们采取不同的方法：

• 首次蒙特卡洛政策评估

对于每一集的策略（可能是我们在前几篇文章中使用的随机策略），只有代理第一次到达S时才算：

• EverEvery访问蒙特卡洛政策评估

对于每一集的策略（可能是我们在前几篇文章中使用的随机策略），代理每次到达S都会计数：

• 增量蒙特卡洛更新

对于剧集中的每个状态St，都有一个奖励Gt，对于每次出现St，状态的平均值V（St）由以下公式计算：

时间差异学习

蒙特卡洛强化学习算法克服了由未知模型引起的策略估计困难。然而，缺点是该策略只能在整个事件后更新。

换句话说，蒙特卡洛方法没有充分利用MDP学习任务结构。幸运的是，这就是更有效的时间差（TD）方法发挥作用的地方，充分利用了MDP结构。

时间差分学习：深度编程和蒙特卡洛的结合

众所周知，蒙特卡罗方法需要等到事件结束才能确定V（St）。另一方面，时间差或TD方法只需要等到下一个时间步。

也就是说，在时间t+1，TD方法使用观察到的奖励Rt+1，并立即形成TD目标R（t+1）+V（St+1），用TD误差更新V（St）（我们将在下面定义）。

在解决了蒙特卡洛的缺点之后，我们准备进一步讨论时间差分学习。著名的Q学习算法属于TD方法，但让我们从最简单的TD（0）开始。

TD（0）

在蒙特卡洛，Gt是完整事件的实际回报。现在，如果我们用估计的返回值R（t+1）+V（St+1）替换Gt，这就是TD（0）的样子：

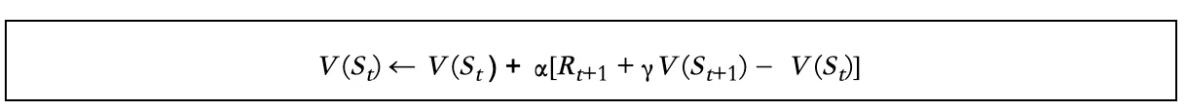
哪里：

• R（t+1）+V（St+1）称为TD目标值
• R（t+1）+V（St+1）-V（St）称为TD误差。

MC使用精确的返回Gt来更新值，而TD使用贝尔曼最优方程来估计值，然后用目标值更新估计值。

总结

你成功了！从这篇文章中，我希望你已经掌握了以下基本知识：

• MC：蒙特卡洛学习
• TD：时间差异学习
• 最简单的TD学习，TD（0）

下一次，我们将介绍一个更复杂的TD学习，TD（），它将直接引导我们进行Q学习。

感谢您的阅读！如果你喜欢这篇文章，请尽可能多地点击拍手按钮。这将意味着很多，并鼓励我继续分享我的知识。